Graph traversals in AQL

General query idea

This query is only useful if you use edge collections and/or graphs in your data model. It is supposed to walk through your graph. Therefore it starts at one specific document (start-vertex) and follows all edges connected to this document. For all documents (vertices) that are targeted by these edges it will again follow all edges connected to them and so on. It is possible to define how many of these follow iterations should be executed at least (min-depth) and at most (max-depth). For all vertices that where visited during this process in the range between min-depth and max-depth iterations you will get a result in form of a set with three items:

1. The visited vertex.
2. The edge pointing to it
3. The complete path from start-vertex to the visited vertex as a JSON document with an attribute edges and an attribute vertices, each a list of the coresponding elements. These lists are sorted, s.t. the first element in vertices is the start-vertex and the last is the visited vertex. And that the n-th element in edges connects the n-th element with the (n+1)-th element in vertices.

Example execution

Let’s take a look at a simple example to explain how it works. This is the graph that we are going to traverse:

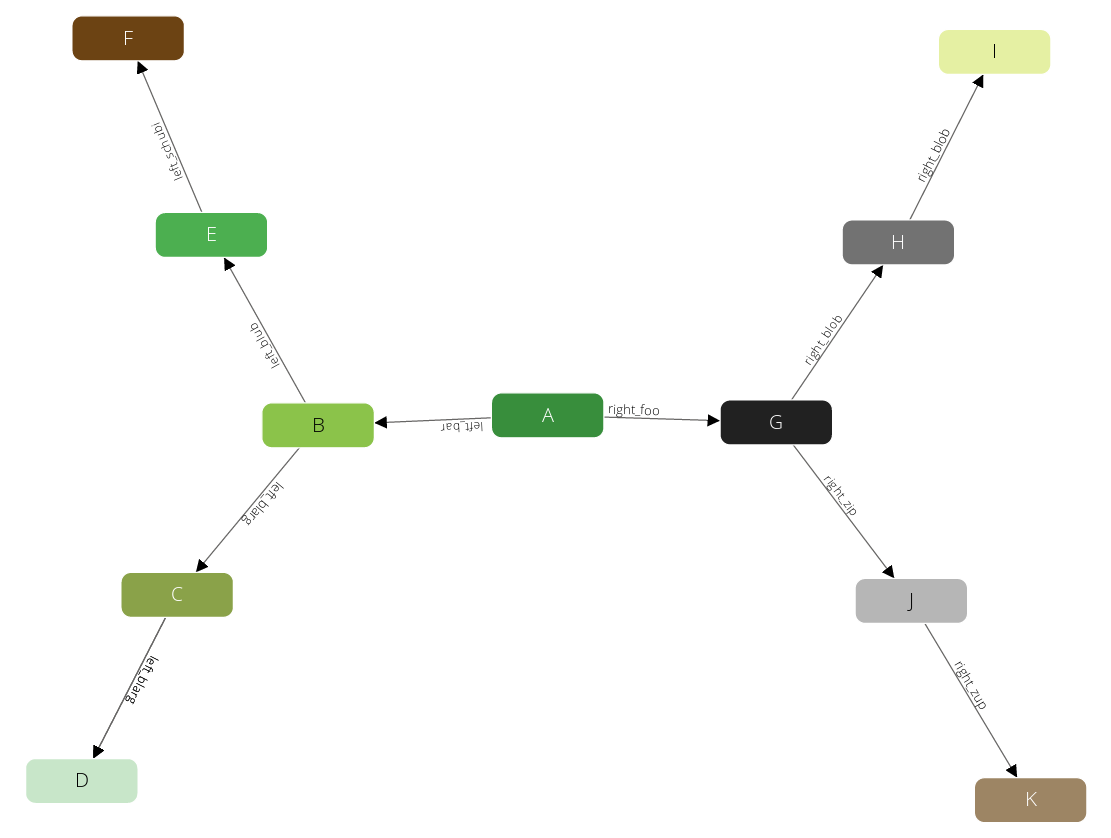
Now we use the following parameters for our query:

1. We start at the vertex A.
2. We use a min-depth of 1.
3. We use a max-depth of 2.
4. We follow only outbound direction of edges

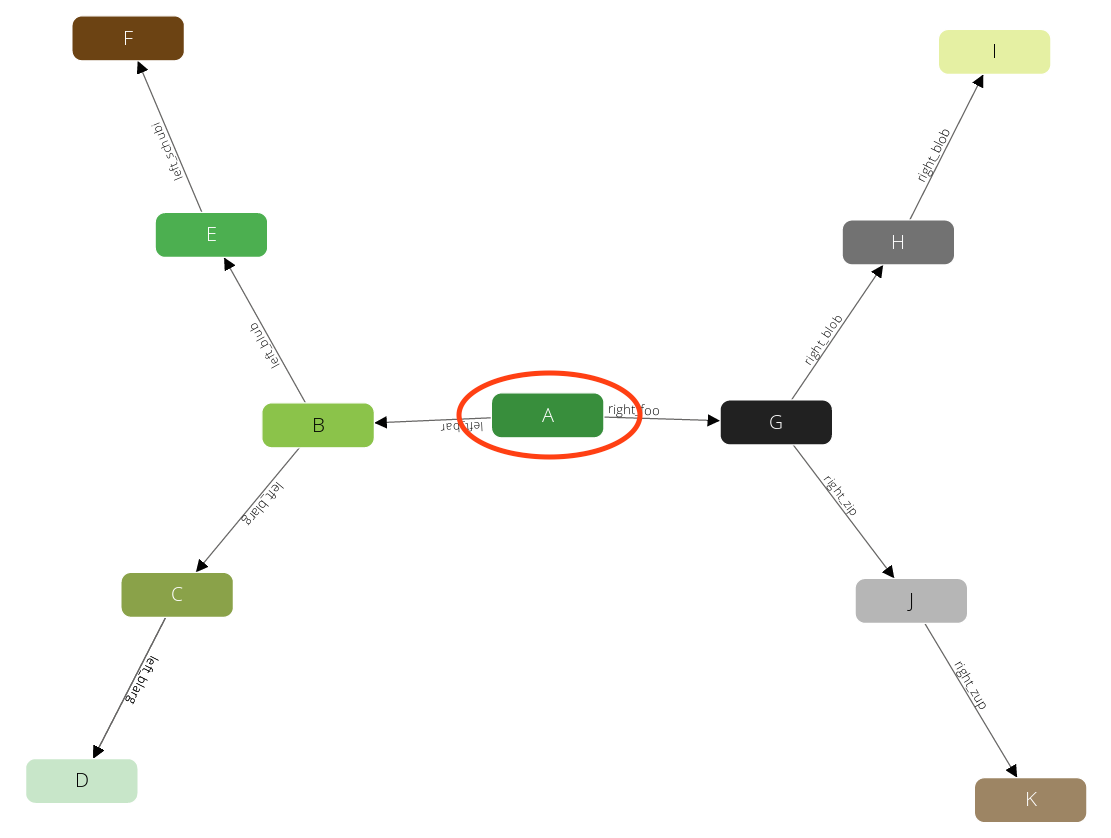
Now it walks to one of the direct neighbors of A, say B (NOTE: ordering is not guaranteed):

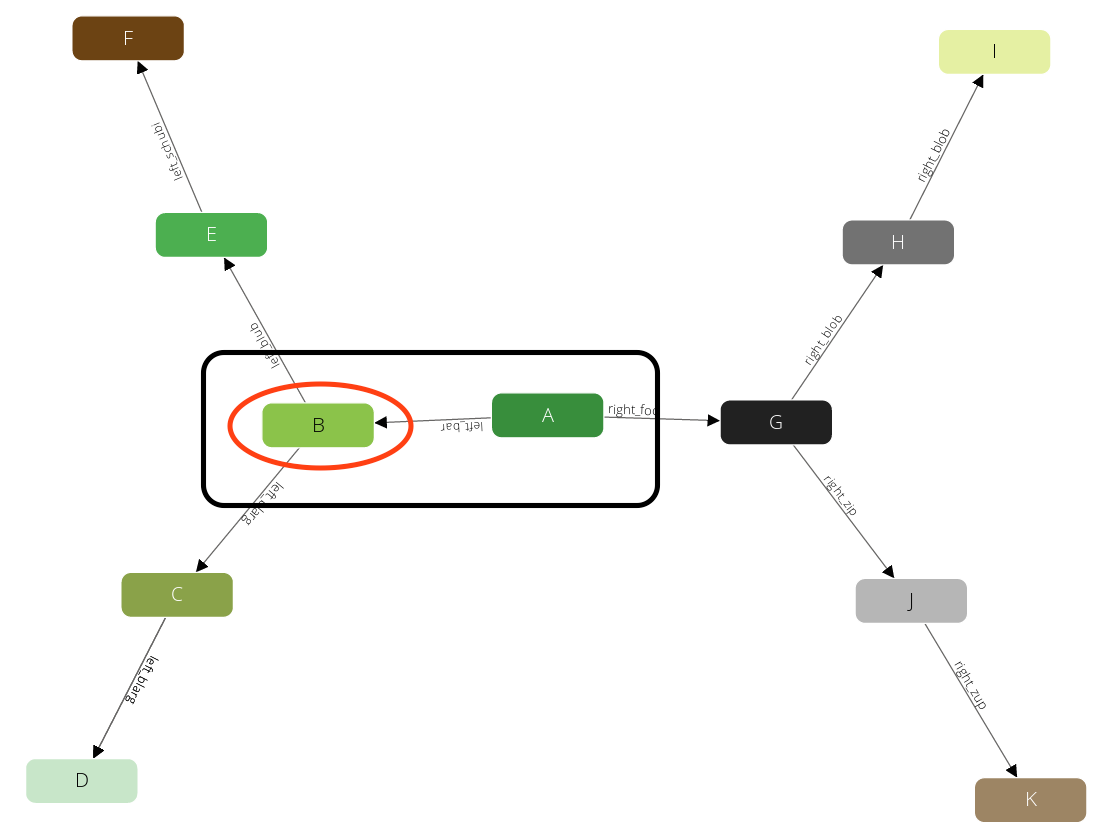
The query will remember the state (red circle) and will emit the first result A -> B (black box). This will also prevent the traverser to be trapped in cycles. Now again it will visit one of the direct neighbors of B, say E:

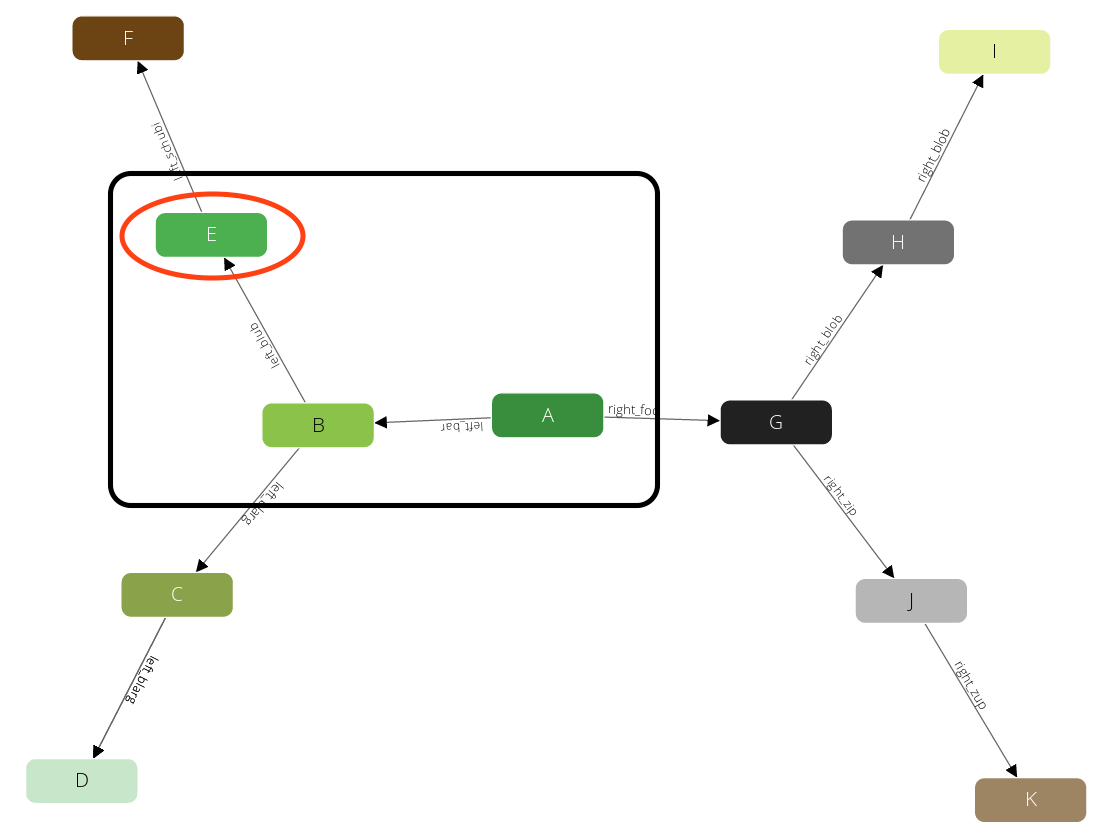
We have limited the query with a max-depth of 2 then it will not pick any neighbor of E as the path from A to E already requires 2 steps. Instead we will go back one level to B and continue with any other direct neighbor there:

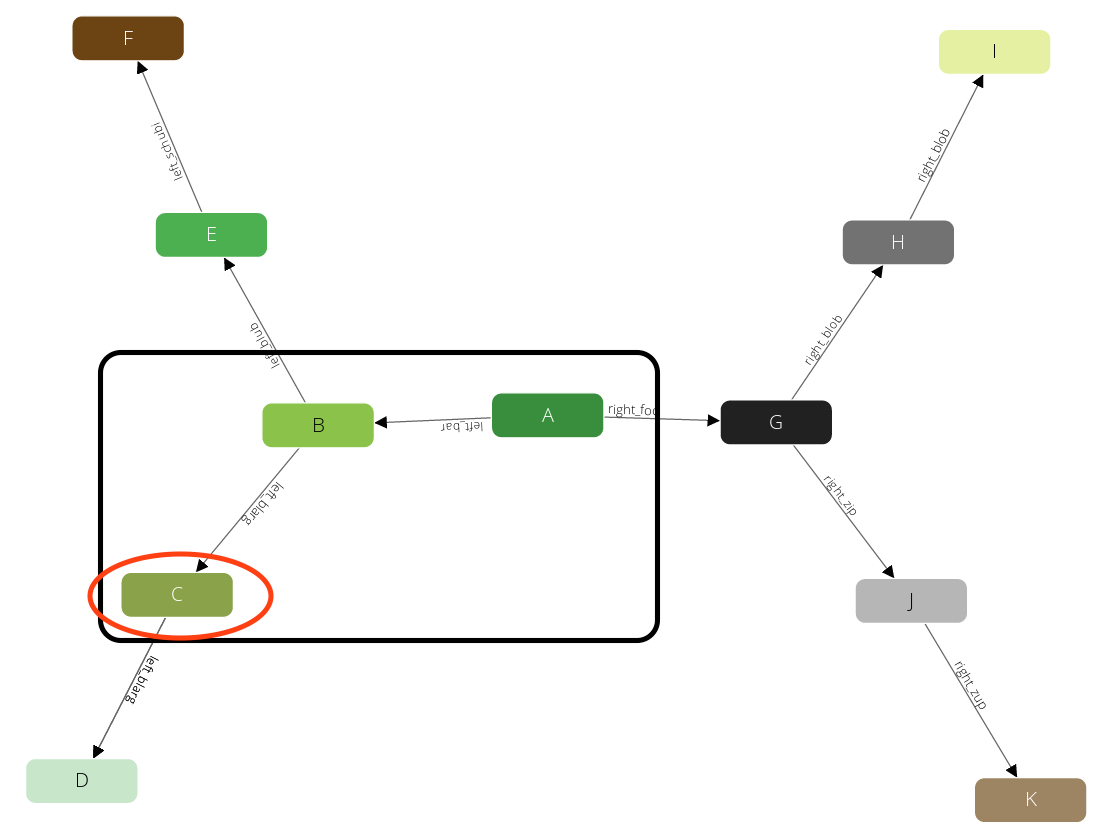
Again after we produced this result we will step back to B. But there is no neighbor of B left that we have not yet visited. Hence we go another step back to A and continue with any other neighbor there.

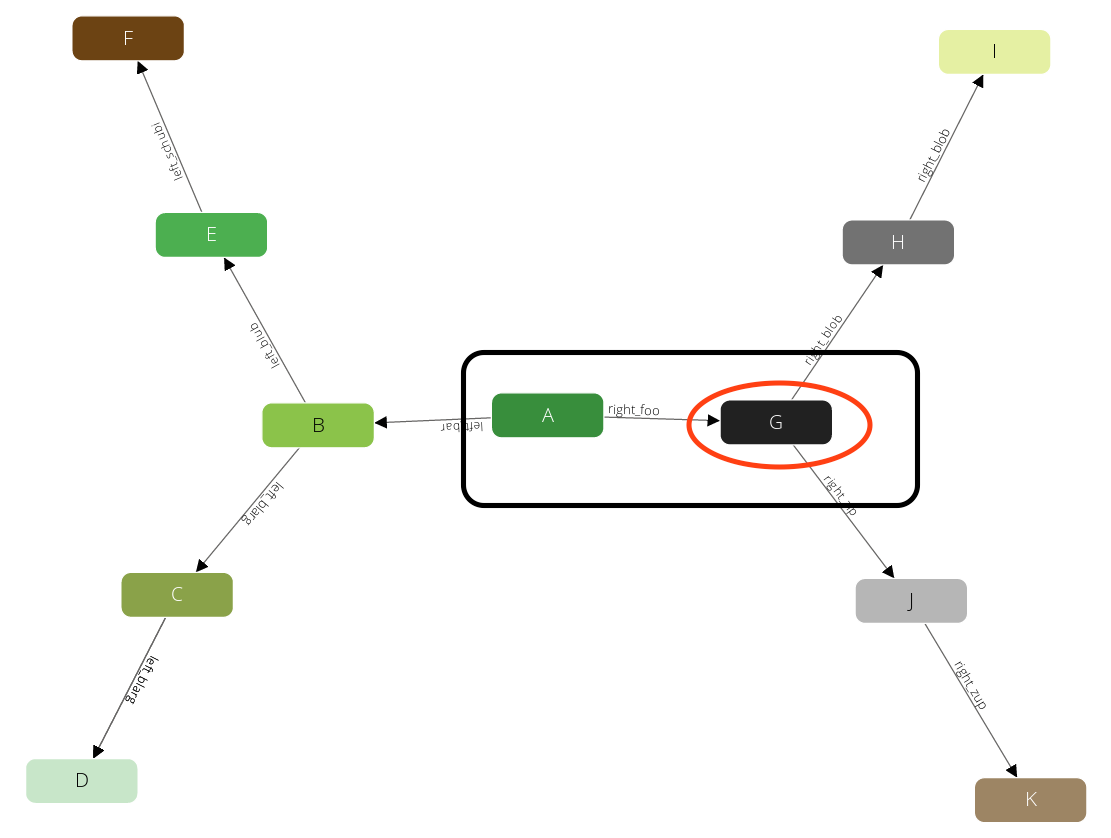
And identical to the iterations before we will visit H:

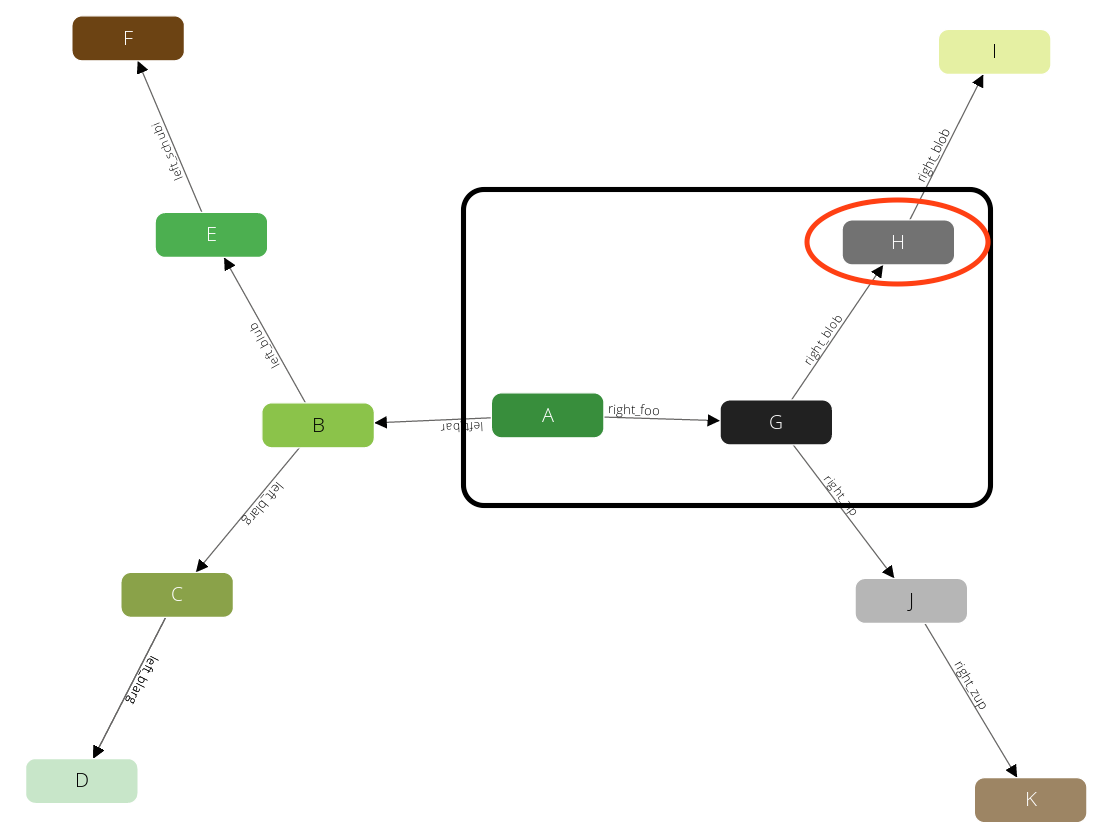
And J:

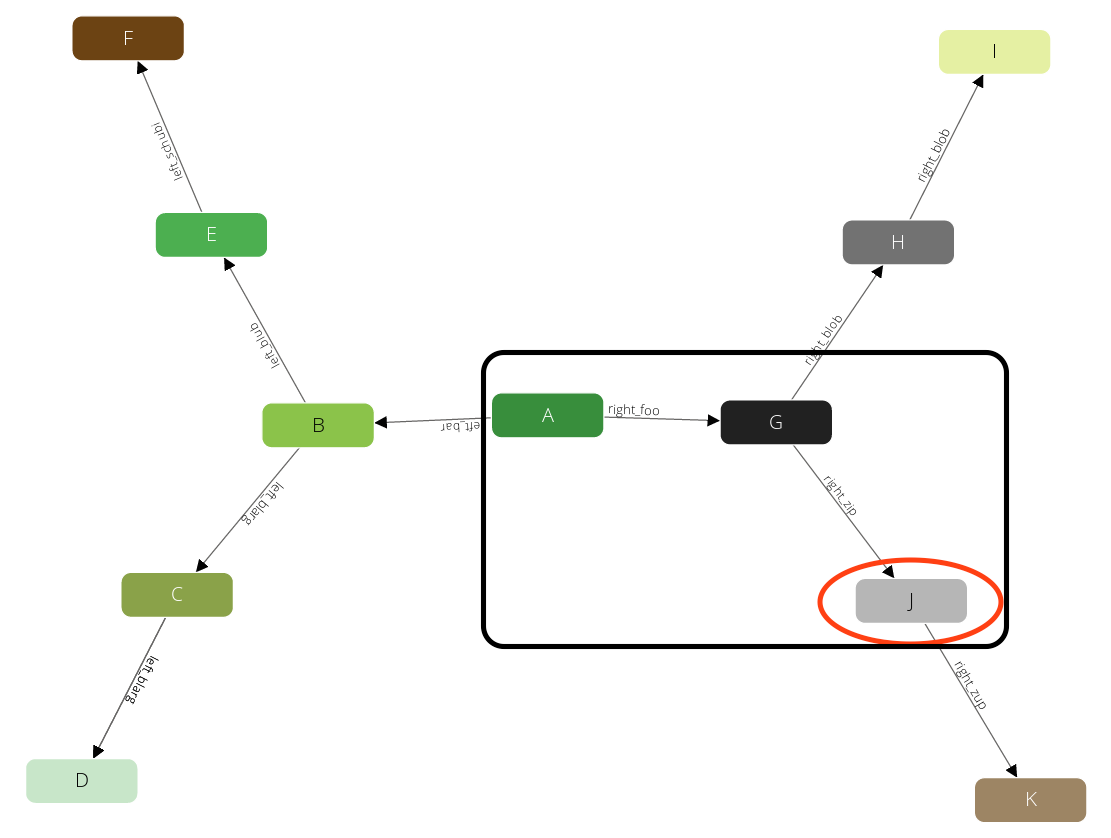
And after these steps there is no further result left. So all together this query has returned the following paths:

1. A -> B
2. A -> B -> E
3. A -> B -> C
4. A -> G
5. A -> G -> H
6. A -> G -> J

Syntax

Now let’s see how we can write a query that follows this schema. You have two options here, you can either use a named graph (see the graphs chapter on how to create it) or anonymous graphs.

Working on named graphs:

FOR vertex[, edge[, path]] IN MIN[..MAX] OUTBOUND|INBOUND|ANY startVertex GRAPH graphName

• FOR - emits up to three variables:
  • vertex: the current vertex in a traversal
  • edge: (optional) the current edge in a traversal
  • path: (optional, requires edge to be present) an object representing the current path with two members:
    • vertices: an array of all vertices on this path.
    • edges: an array of all edges on this path.
• IN MIN..MAX OUTBOUND startVertex GRAPH graphName
  • OUTBOUND|INBOUND|ANY traversal will be done for outbound / inbound / inbound+outbound pointing edges
  • startVertex: one vertex where the traversal will originate from, this can be specified in the form of an id string or in the form of a document with the attribute _id. All other values will lead to a warning and an empty result. If the specified id does not exist, the result is empty as well and there is no warning.
  • graphName: the name identifying the named graph. It’s vertex and edge collections will be looked up.
  • MIN: edges and vertices returned by this query will start at the traversal depth of MIN (thus edges and vertices below will not be returned). If not specified, defaults to 1, which is the minimal possible value.
  • MAX: up to MAX length paths are traversed. If omitted in the query, MAX equals MIN. Thus only the vertices and edges in the range of MIN are returned.

Working on collection sets:

FOR vertex[, edge[, path]] IN MIN[..MAX] OUTBOUND|INBOUND|ANY startVertex edgeCollection1, .., edgeCollectionN

Instead of the GRAPH graphName you may specify a list of edge collections. Vertex collections are evaluated from the edges. The rest of the behavior is similar to the named version.

Working on collection sets with mixed directions:

For traversals with a list of edge collections you can optionally specify the direction for some of the edge collections. Say for example you have three edge collections edges1, edges2 and edges3, where in edges2 the direction has no relevance but in edges1 and edges3 the direction should be taken into account. In this case you can use OUTBOUND as general traversal direction and ANY specifically for edges2 in the following statement:

FOR vertex IN OUTBOUND startVertex edges1, ANY edges2, edges3

All collections in the list that do not specify their own direction will use the direction defined after IN. This allows to use a different direction for each collection in your traversal.

Using filters and the explainer to extrapolate the costs

All three variables emitted by the traversals might as well be used in filter statements. For some of these filter statements the optimizer can detect that it is possible to prune paths of traversals earlier, hence filtered results will not be emitted to the variables in the first place. This may significantly improve the performance of your query. Whenever a filter is not fulfilled the complete set of vertex, edge and path will be skipped. All paths with a length greater than MAX will never be computed.

In the current state OR combined filters cannot be optimized, AND combined filters can.

Filtering on paths

This allows for the most powerful filtering and may have the highest impact on performance. Using the path variable you can filter on specific iteration depths. You can filter for absolute positions in the path by (specifying a positive number) (which then qualifies for the optimizations) or relative positions to the end of the path by specifying a negative number. Note: In the current state there is no way to define a filter for all elements on the path. This will be added in the future.

Filtering edges on the path

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
  FILTER p.edges[0].theTruth == true
  RETURN p

will filter all paths where the start edge (# 0) has the attribute theTruth equaling true. The resulting paths will be up to 5 items long.

Filtering vertices on the path

Similar to filtering the edges on the path you can also filter the vertices:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
  FILTER p.vertices[1]._key == "G"
  RETURN p

Combining several filters

And of course you can combine these filters in any way you like:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
  FILTER p.edges[0].theTruth == true
  AND p.edges[1].theFalse == false
  FILTER p.vertices[1]._key == "G"
  RETURN p

will filter all paths where the first edge has the attribute theTruth equaling true, the first vertex is “G” and the second edge has the attribute theFalse equaling false. The resulting paths will be up to 5 items long. Note here: Although we have defined a MIN of 1 we will only get results of depth 2. This is because for all results in depth 1 the second edge does not exist and hence cannot fulfill the condition.

Examples

We will create a simple symmetric traversal demonstration graph:

arangosh> var examples = require("org/arangodb/graph-examples/example-graph.js");
arangosh> var graph = examples.loadGraph("traversalGraph");
arangosh> db.circles.toArray();
arangosh> db.edges.toArray();

[ 
  { 
    "label" : "5", 
    "_id" : "circles/E", 
    "_rev" : "526665857", 
    "_key" : "E" 
  }, 
  { 
    "label" : "6", 
    "_id" : "circles/F", 
    "_rev" : "526862465", 
    "_key" : "F" 
  }, 
  { 
    "label" : "3", 
    "_id" : "circles/C", 
    "_rev" : "526272641", 
    "_key" : "C" 
  }, 
  { 
    "label" : "11", 
    "_id" : "circles/K", 
    "_rev" : "527845505", 
    "_key" : "K" 
  }, 
  { 
    "label" : "4", 
    "_id" : "circles/D", 
    "_rev" : "526469249", 
    "_key" : "D" 
  }, 
  { 
    "label" : "9", 
    "_id" : "circles/I", 
    "_rev" : "527452289", 
    "_key" : "I" 
  }, 
  { 
    "label" : "1", 
    "_id" : "circles/A", 
    "_rev" : "525879425", 
    "_key" : "A" 
  }, 
  { 
    "label" : "2", 
    "_id" : "circles/B", 
    "_rev" : "526076033", 
    "_key" : "B" 
  }, 
  { 
    "label" : "10", 
    "_id" : "circles/J", 
    "_rev" : "527648897", 
    "_key" : "J" 
  }, 
  { 
    "label" : "7", 
    "_id" : "circles/G", 
    "_rev" : "527059073", 
    "_key" : "G" 
  }, 
  { 
    "label" : "8", 
    "_id" : "circles/H", 
    "_rev" : "527255681", 
    "_key" : "H" 
  } 
]
[ 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zip", 
    "_id" : "edges/529877121", 
    "_rev" : "529877121", 
    "_key" : "529877121", 
    "_from" : "circles/G", 
    "_to" : "circles/J" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zup", 
    "_id" : "edges/530073729", 
    "_rev" : "530073729", 
    "_key" : "530073729", 
    "_from" : "circles/J", 
    "_to" : "circles/K" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blarg", 
    "_id" : "edges/528500865", 
    "_rev" : "528500865", 
    "_key" : "528500865", 
    "_from" : "circles/B", 
    "_to" : "circles/C" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_schubi", 
    "_id" : "edges/529090689", 
    "_rev" : "529090689", 
    "_key" : "529090689", 
    "_from" : "circles/E", 
    "_to" : "circles/F" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_bar", 
    "_id" : "edges/528304257", 
    "_rev" : "528304257", 
    "_key" : "528304257", 
    "_from" : "circles/A", 
    "_to" : "circles/B" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blub", 
    "_id" : "edges/529680513", 
    "_rev" : "529680513", 
    "_key" : "529680513", 
    "_from" : "circles/H", 
    "_to" : "circles/I" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blub", 
    "_id" : "edges/528894081", 
    "_rev" : "528894081", 
    "_key" : "528894081", 
    "_from" : "circles/B", 
    "_to" : "circles/E" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blorg", 
    "_id" : "edges/528697473", 
    "_rev" : "528697473", 
    "_key" : "528697473", 
    "_from" : "circles/C", 
    "_to" : "circles/D" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blob", 
    "_id" : "edges/529483905", 
    "_rev" : "529483905", 
    "_key" : "529483905", 
    "_from" : "circles/G", 
    "_to" : "circles/H" 
  }, 
  { 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_foo", 
    "_id" : "edges/529287297", 
    "_rev" : "529287297", 
    "_key" : "529287297", 
    "_from" : "circles/A", 
    "_to" : "circles/G" 
  } 
]

To get started we select the full graph; for better overview we only return the vertex ids:

arangosh> db._query("FOR v IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' RETURN v._key");
arangosh> db._query("FOR v IN 1..3 OUTBOUND 'circles/A' edges RETURN v._key");

[ 
  "B", 
  "C", 
  "D", 
  "E", 
  "F", 
  "G", 
  "H", 
  "I", 
  "J", 
  "K" 
]
[object ArangoQueryCursor, count: 10, hasMore: false]
[ 
  "B", 
  "C", 
  "D", 
  "E", 
  "F", 
  "G", 
  "H", 
  "I", 
  "J", 
  "K" 
]
[object ArangoQueryCursor, count: 10, hasMore: false]

We can nicely see its heading for the first outer vertex, then going back to the branch to descend into the next tree. After that it returns to our start node, to descend again. As we can see both queries return the same result, the first one uses the named graph, the second directly uses the edge collection.

Now we only want the elements of a specific depth - 2 - the ones that are right behind the fork:

arangosh> db._query("FOR v IN 2..2 OUTBOUND 'circles/A' GRAPH 'traversalGraph' return v._key");
arangosh> db._query("FOR v IN 2 OUTBOUND 'circles/A' GRAPH 'traversalGraph' return v._key");

[ 
  "C", 
  "E", 
  "H", 
  "J" 
]
[object ArangoQueryCursor, count: 4, hasMore: false]
[ 
  "C", 
  "E", 
  "H", 
  "J" 
]
[object ArangoQueryCursor, count: 4, hasMore: false]

As you can see, we can express this in two ways, one is to omit the MAX parameter of the expression.

Filter examples

Now lets start to add some filters. We want to cut of the branch on the right side of th graph, we may filter in two ways:

• we know the vertex at depth 1 has _key == G
• we know the label attribute of the edge connecting A to G is right_foo

arangosh> db._query("FOR v, e, p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.vertices[1]._key != 'G' RETURN v._key");
arangosh> db._query("FOR v, e, p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.edges[0].label != 'right_foo' RETURN v._key");

[ 
  "B", 
  "C", 
  "D", 
  "E", 
  "F" 
]
[object ArangoQueryCursor, count: 5, hasMore: false]
[ 
  "B", 
  "C", 
  "D", 
  "E", 
  "F" 
]
[object ArangoQueryCursor, count: 5, hasMore: false]

As we can see all vertices behind G are skipped in both queries. The first filters on the vertex _key, the second on an edge label. Note again as soon as a filter is not fulfilled for any of the three elements v, e or p the complete set of these will be excluded from the result.

We also may combine several filters, for instance to filter out the right branch (G), and the E branch:

arangosh> db._query("FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.vertices[1]._key != 'G' FILTER p.edges[1].label != 'left_blub' return v._key");
arangosh> db._query("FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.vertices[1]._key != 'G' AND    p.edges[1].label != 'left_blub' return v._key");

[ 
  "B", 
  "C", 
  "D" 
]
[object ArangoQueryCursor, count: 3, hasMore: false]
[ 
  "B", 
  "C", 
  "D" 
]
[object ArangoQueryCursor, count: 3, hasMore: false]

As you can see combining two FILTER statements with an AND has the same result.

Comparing OUTBOUND / INBOUND / ANY

All our previous examples traversed the graph into outbound edge directions. You may however want to also traverse in reverse direction (INBOUND) or both (ANY), Since circles/A only has outbound edges, we start our queries from circles/E:

arangosh> db._query("FOR v IN 1..3 OUTBOUND 'circles/E' GRAPH 'traversalGraph' return v._key");
arangosh> db._query("FOR v IN 1..3 INBOUND 'circles/E' GRAPH 'traversalGraph' return v._key");
arangosh> db._query("FOR v IN 1..3 ANY 'circles/E' GRAPH 'traversalGraph' return v._key");

[ 
  "F" 
]
[object ArangoQueryCursor, count: 1, hasMore: false]
[ 
  "B", 
  "A" 
]
[object ArangoQueryCursor, count: 2, hasMore: false]
[ 
  "B", 
  "A", 
  "G", 
  "C", 
  "D", 
  "F" 
]
[object ArangoQueryCursor, count: 6, hasMore: false]

The first traversal will only walk into the forward (OUTBOUND) direction. Therefore from E we only can see F. Walking into reverse direction (INBOUND) we see the path to A: B, A. Walking in forward and reverse direction (ANY) we can see a more diverse result. First of all we see the simple paths to F and A. However these vertices have edges in other directions and they will be traversed. Note here: The traverser may use identical edges multiple times. For instance if it walks from E to F it will continue to walk from F to E using the same edge once again. Due to this we will see duplicate nodes in the result.

Use the AQL explainer for optimizations

Now lets have a look what the optimizer does behind the curtains and inspect traversal queries using the explainer:

arangosh> db._explain("FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' LET localScopeVar = RAND() > 0.5 FILTER p.edges[0].theTruth != localScopeVar RETURN v._key", {}, {colors: false});
arangosh> db._explain("FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.edges[0].label == 'right_foo' RETURN v._key", {}, {colors: false});

Query string:
 FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' LET localScopeVar = RAND() > 0.5 
 FILTER p.edges[0].theTruth != localScopeVar RETURN v._key

Execution plan:
 Id   NodeType          Est.   Comment
  1   SingletonNode        1   * ROOT
  2   TraversalNode        1     - FOR v  /* vertex */  , e  /* edge */  , p  /* paths */  IN 1..3  /* min..maxPathDepth */  OUTBOUND 'circles/A' /* startnode */  GRAPH 'traversalGraph'
  3   CalculationNode      1     - LET localScopeVar = (RAND() > 0.5)   /* simple expression */
  4   CalculationNode      1     - LET #4 = (p.`edges`[0].`theTruth` != localScopeVar)   /* simple expression */
  5   FilterNode           1     - FILTER #4
  6   CalculationNode      1     - LET #6 = v.`_key`   /* attribute expression */
  7   ReturnNode           1     - RETURN #6

Indexes used:
 none

Traversals on graphs:
 Id   Depth   Vertex collections   Edge collections   Filter conditions
  2   1..3    circles              edges              

Optimization rules applied:
 Id   RuleName
  1   move-calculations-up
  2   move-calculations-down


Query string:
 FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph' FILTER p.edges[0].label == 'right_foo' 
 RETURN v._key

Execution plan:
 Id   NodeType          Est.   Comment
  1   SingletonNode        1   * ROOT
  2   TraversalNode        1     - FOR v  /* vertex */  , e  /* edge */  , p  /* paths */  IN 1..3  /* min..maxPathDepth */  OUTBOUND 'circles/A' /* startnode */  GRAPH 'traversalGraph'
  3   CalculationNode      1     - LET #3 = (p.`edges`[0].`label` == "right_foo")   /* simple expression */
  4   FilterNode           1     - FILTER #3
  5   CalculationNode      1     - LET #5 = v.`_key`   /* attribute expression */
  6   ReturnNode           1     - RETURN #5

Indexes used:
 none

Traversals on graphs:
 Id   Depth   Vertex collections   Edge collections   Filter conditions
  2   1..3    circles              edges              `Path`.`edges`[0] -> e.`label` == "right_foo"

Optimization rules applied:
 Id   RuleName
  1   move-calculations-up
  2   move-filters-up
  3   move-calculations-up-2
  4   move-filters-up-2
  5   merge-traversal-filter

We now see two queries, in one we add a variable localScopeVar which is outside the scope of the traversal itself - it is not known inside of the traverser. Therefore this filter can only executed after the traversal, which may be undesired in large graphs. The second query on the other hand only operates on the path, and therefore this condition can be used during the execution of the traversal, paths that are filtered out by this condition won’t be processed at all.

And finally clean it up again:

arangosh> var examples = require("org/arangodb/graph-examples/example-graph.js");
arangosh> examples.dropGraph("traversalGraph");

true

If this traversal is not powerful enough for your needs, so you cannot describe your conditions as AQL filter statements you might want to look at manually crafted traverser.

See here for more traversal examples.